Skip to content

MANE 6313

Week 14, Module C

Student Learning Outcome

  • Select an appropriate experimental design with one or more factors,
  • Select an appropriate model with one or more factors,
  • Evaluate statistical analyses of experimental designs,
  • Assess the model adequacy of any experimental design, and
  • Interpret model results.

Module Learning Outcome

Explain mixture designs.

Resources for the Week 14, Module C micro-lecture are:

Introduction to Mixture Designs

  • In previous situations, we have assumed that the levels of each factor are independent of the levels of all the other factors

  • This assumption does not hold in mixture experiments

  • Usually there is a restriction that the sum of components equals one

  • Examine Figure 11--39 on page 543

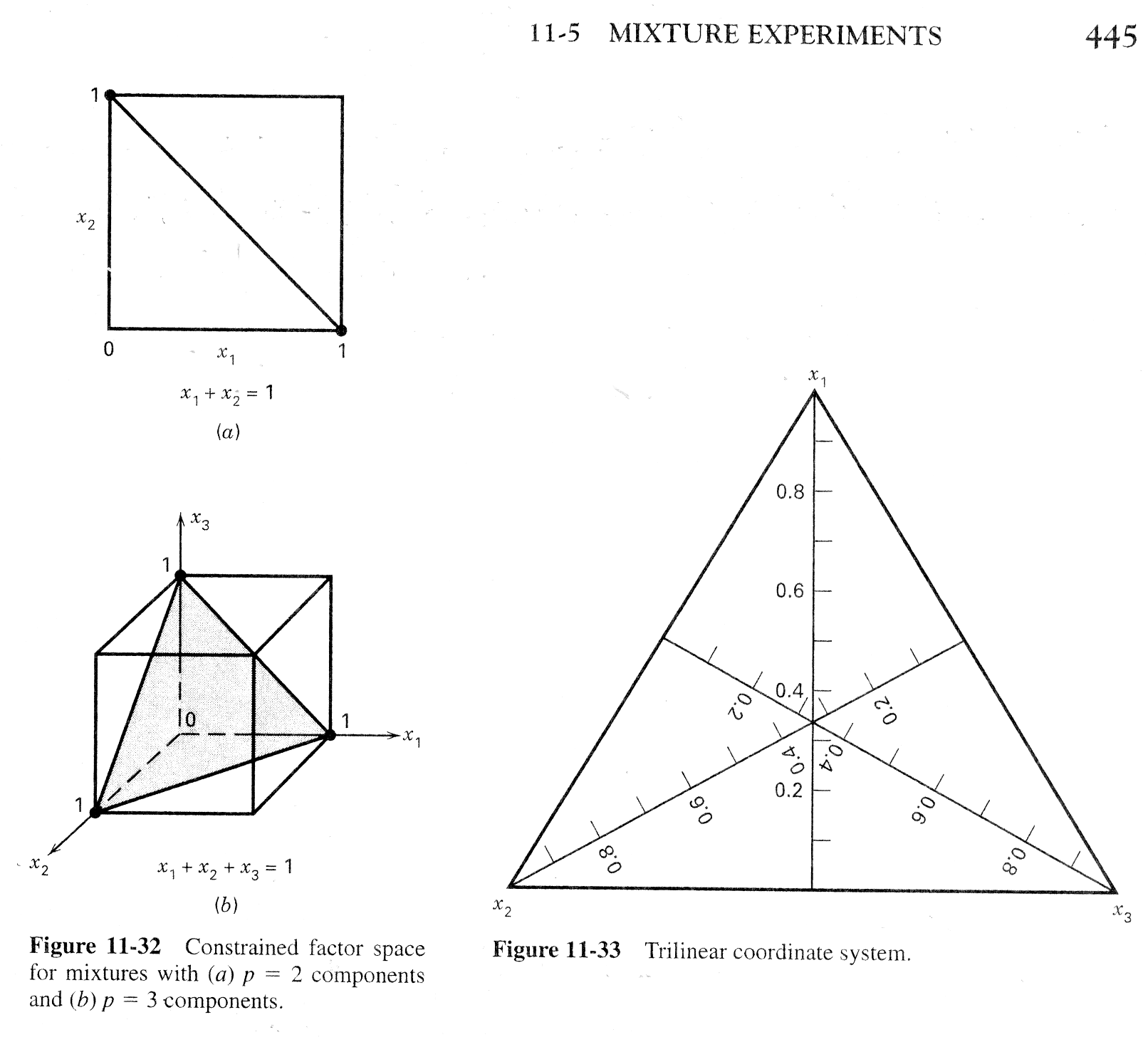
figure 11.32

Simplex Lattice Designs

  • A \(\left\{p,m\right\}\) lattice design for \(p\) components consists of \(m+1\) equally spaced values from 0 to 1
\[ x_i=0,\frac{1}{m},\frac{2}{m},\ldots,1\;\;i=1,2,\ldots,p \]

  • Examine Figure 11-41 on page 543

  • In general, a \({p,m}\) lattice design requires

$$ N=\frac{(p+m-1)!}{m!(p-1)!} $$ points

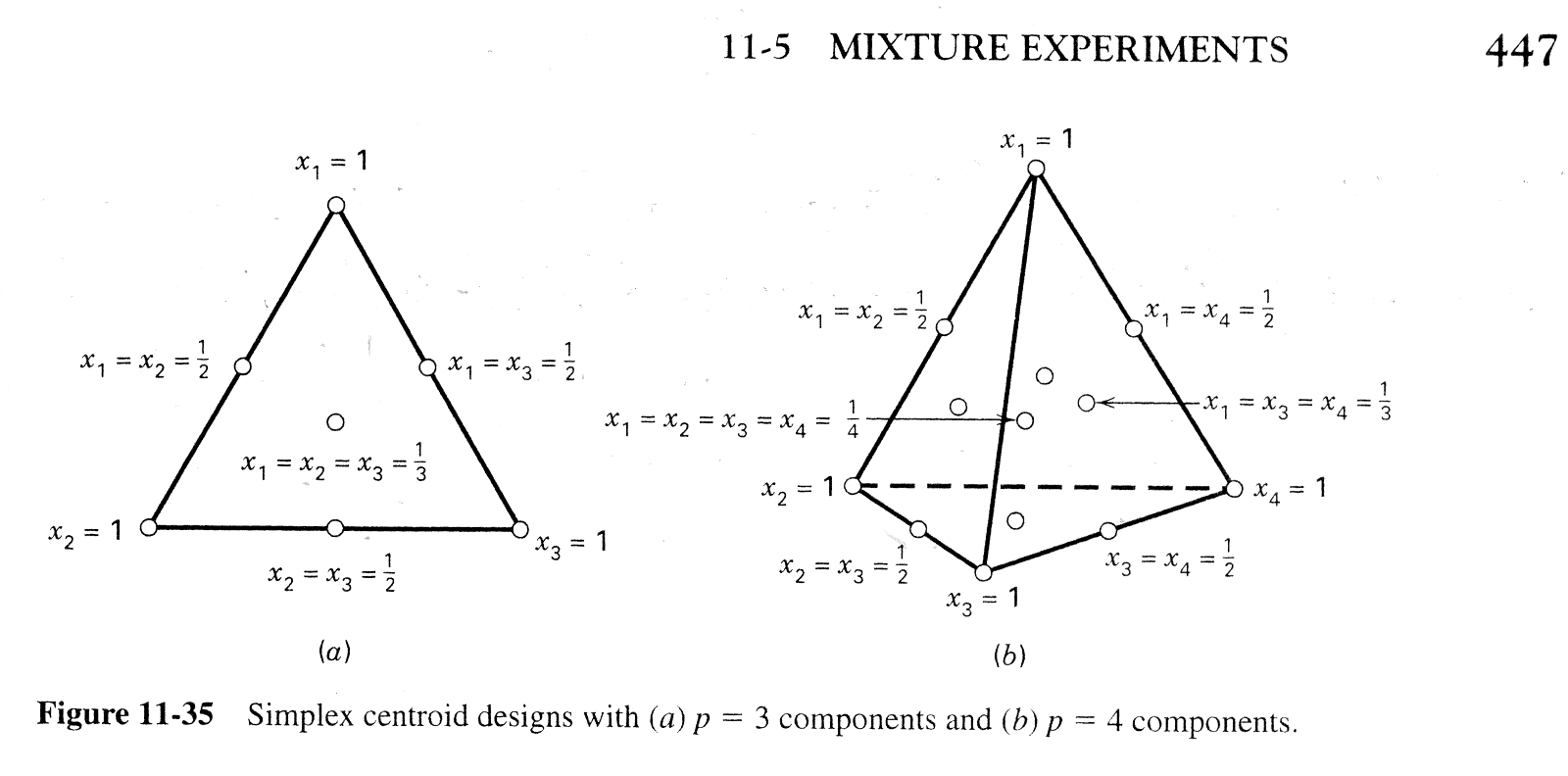
figure 11.35

Simplex Centroid Design

  • A design requiring \(2^p-1\) points corresponding to all permutations of the design points

  • See Figure 11--42 on page 544

  • A Criticism of the simplex designs is that most experiments occur along the boundary of the region and not in the interior of the design

figure 11.35

Mixture Models

  • Recall that \(\sum x_i=1\)

  • Slightly different standard forms

  • Linear model

\[ E(y)=\sum_{i=1}^p\beta_i x_i \]
  • Quadratic model
\[ E(y)=\sum_{i=1}^p\beta_i x_i + \sum\sum_{i<j}^p\beta_{ij}x_ix_j \]
  • Full cubic model
\[ \begin{aligned} E(y)&=&\sum_{i=1}^p\beta_i x_i + \sum\sum_{i<j}^p\beta_{ij}x_ix_j\\ &&+\sum\sum_{i<j}^p\delta_{ij}x_ix_j(x_i-x_j)\\ &&+\sum\sum_{i<j<k}\sum\beta_{ijk}x_ix_jx_k \end{aligned} \]
  • Special Cubic model
\[ \begin{aligned} E(y)&=&\sum_{i=1}^p\beta_i x_i + \sum\sum_{i<j}^p\beta_{ij}x_ix_j\\ &&+\sum\sum_{i<j<k}\sum\beta_{ijk}x_ix_jx_k \end{aligned} \]

Final Comments on Mixture Designs

  • Minitab supports centroid and lattice designs

  • Often require optimal design because of constraints on experimental region

  • Often requires higher-order terms

Minitab Mixture Design Demonstration

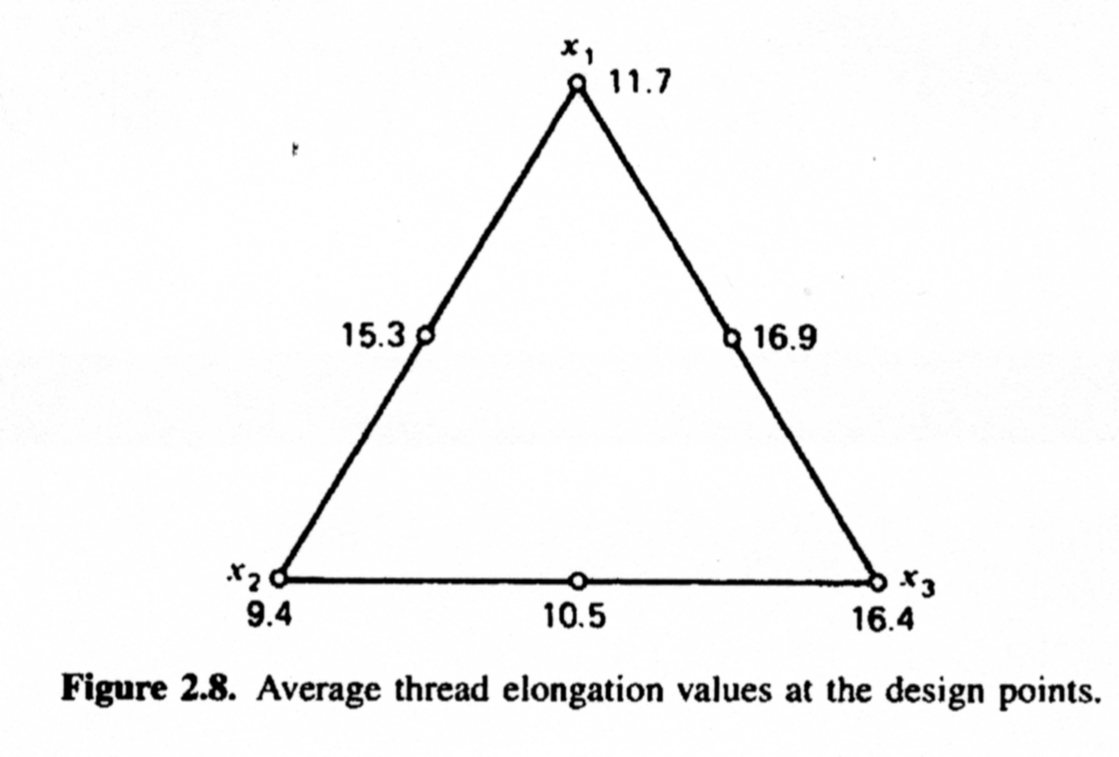
  • Cornell (2002) provides an example of a {3,2} lattice design

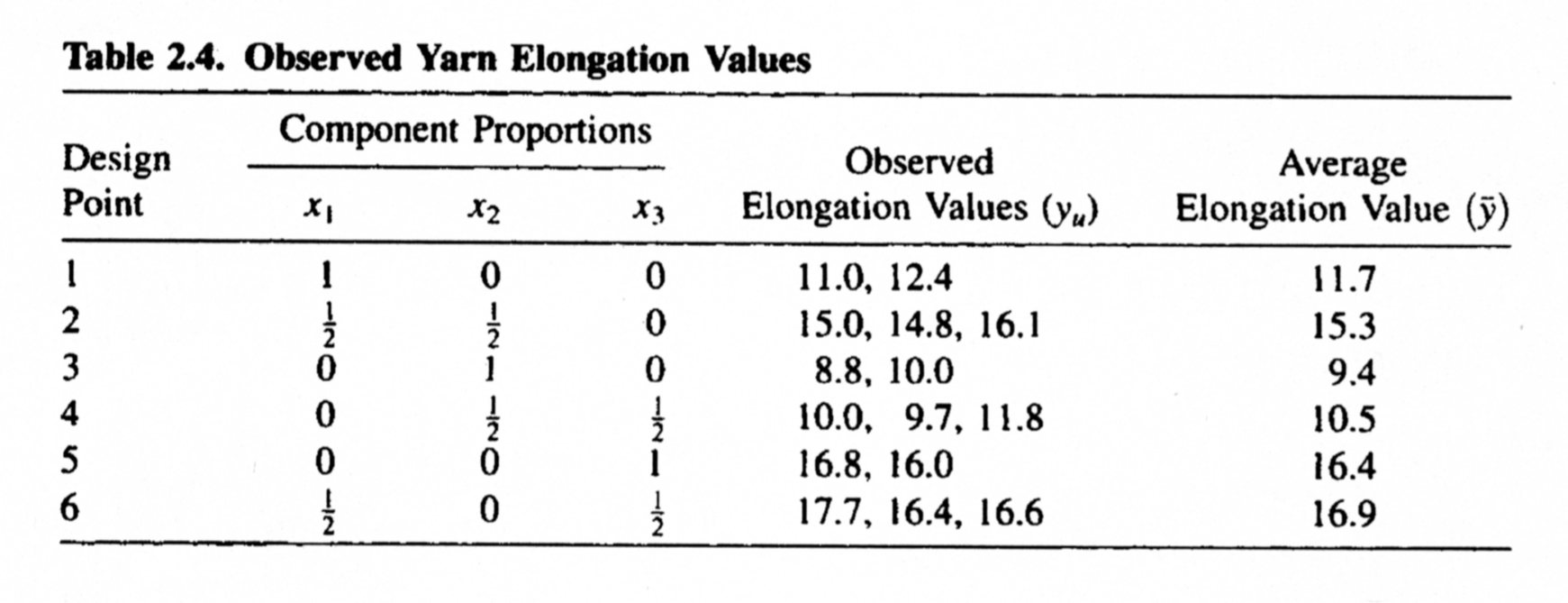
yarn data

Source

  • Design Plot

yarn design

  • Minitab demonstration