MANE 6313
Week 4, Module D
Student Learning Outcome
Analyze simple comparative experiments and experiments with a single factor.
Module Learning Outcome
Assess the assumption of equal variances in one-way analysis of variance.
Resources for the Week 4, Module D micro-lecture are:
Bartlett's Test
\[
\begin{aligned}
H_0&:&\sigma_1^2=\sigma_2^2=\cdots= \sigma_a^2\\
H_1&:&\mbox{above not true for at least one }\sigma_i^2\end{aligned}
\]
- TS:\(\chi^2_0=2.3026\frac{q}{c}\) where
\[
\begin{aligned}
q&=&(N-a)\log_{10}S^2_p-\sum_{i=1}^a(n_i-1)\log_{10}S^2_i\\
c&=&1+\frac{1}{3(a-1)}\left(\sum_{i=1}^a(n_i-1)^{-1}-(N-a)^{-1}\right)\\
S^2_p&=&\frac{\sum_{i=1}^a(n_i-1)S^2_i}{N-1}
\end{aligned}
\]
-
Reject \(H_0\) if \(\chi^2_0>\chi^2_{\alpha,a-1}\)
-
Very sensitive to normality assumption
Bartlett's Test Example Problem
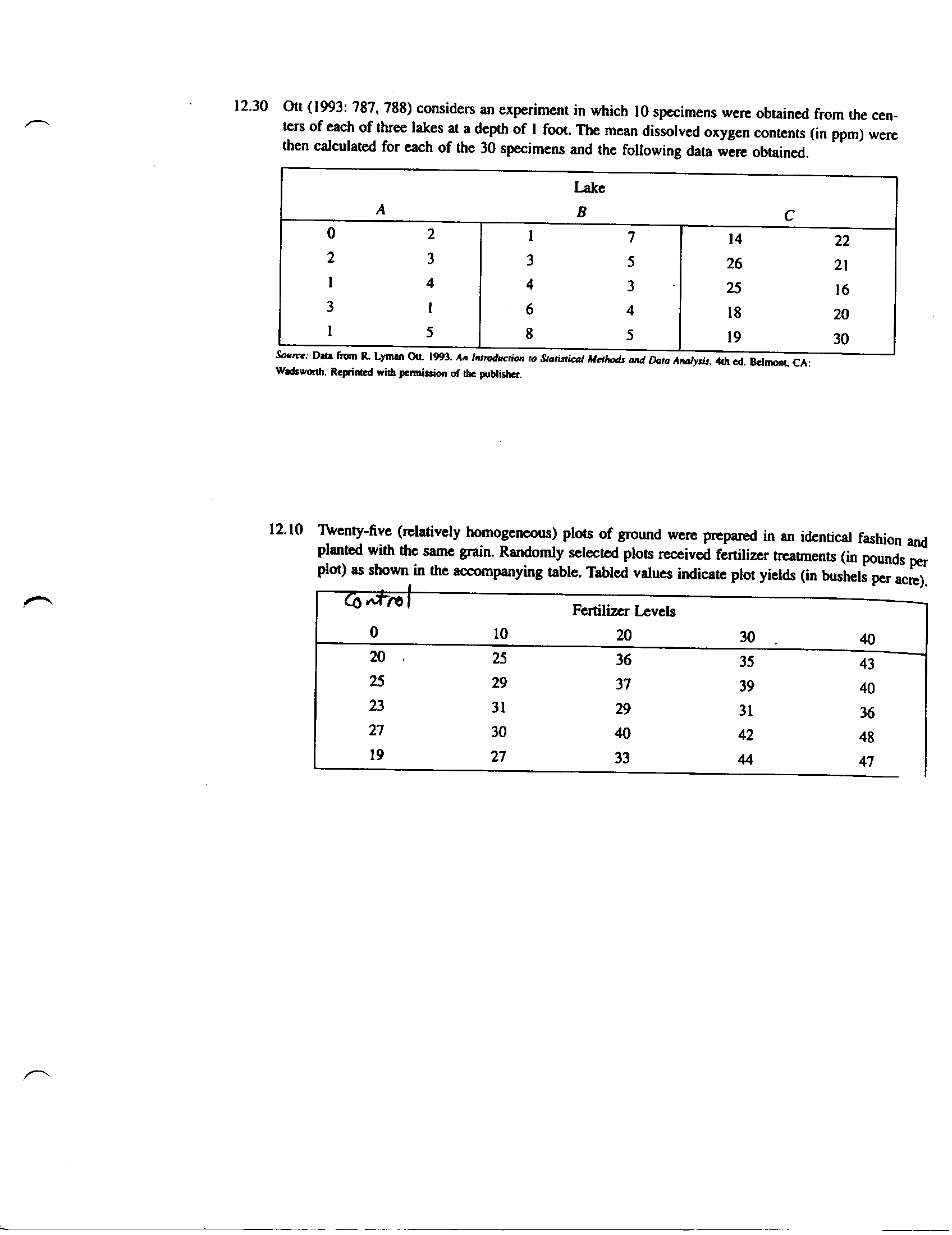
The source for problems 12. 10 and 12.30 is Ostle, Turner, Hicks and McElrath1
Analysis of Variance by Hand

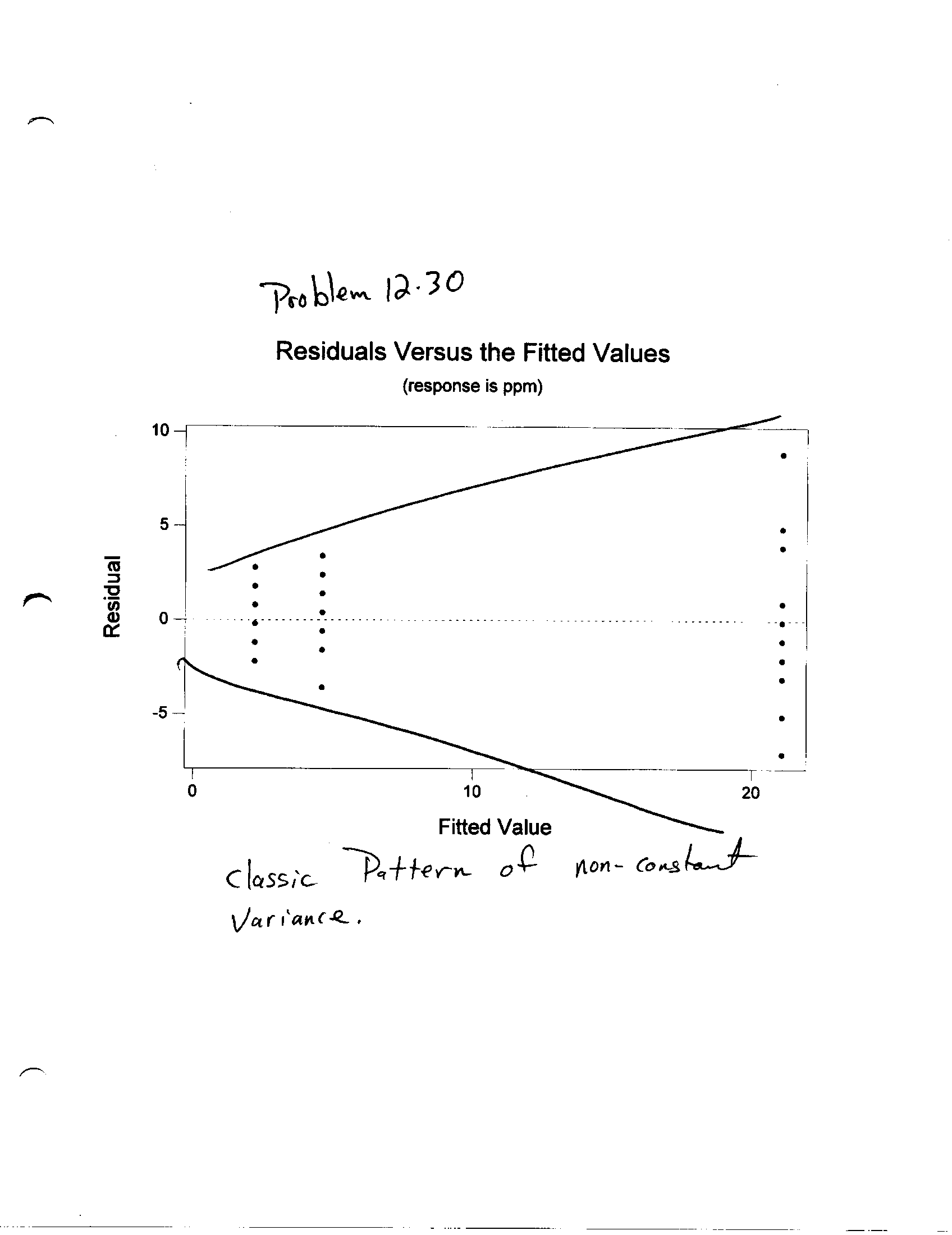
Residual Plot
Bartlett's Test by Hand

Minitab Demonstration
- Bartlett's Test
-
Ostle, Turner, Hicks and McElrath. (1996). Engineering Statistics: The Industrial Experience. Duxbury Press. ↩